NumPy的应用-1Numpy 是一个开源的 Python 科学计算库,用于快速处理任意维度的数组。Numpy 支持常见的数组和矩阵操作,对于同样的数值计算任务,使用 NumPy 不仅代码要简洁的多,而且 NumPy 在性能上也远远优于原生 Python,至少是一到两个数量级的差距,而且数据量越大,NumPy 的优势就越明显。NumPy 最为核心的数据类型是ndarray,使用ndarray可以处理一维、二维和多维数组,该对象相当于是一个快速而灵活的大数据容器。NumPy 底层代码使用 C 语言编写,解决了 GIL 的限制,ndarray在存取数据的时候,数据与数据的地址都是连续的,这确保了可以进行高效率的批量操作,性能上远远优于 Python 中的list;另一方面ndarray对象提供了更多的方法来处理数据,尤其获取数据统计特征的方法,这些方法也是 Python 原生的list没有的。
Numpy 是一个开源的 Python 科学计算库,用于快速处理任意维度的数组。Numpy 支持常见的数组和矩阵操作,对于同样的数值计算任务,使用 NumPy 不仅代码要简洁的多,而且 NumPy 在性能上也远远优于原生 Python,至少是一到两个数量级的差距,而且数据量越大,NumPy 的优势就越明显。
NumPy 最为核心的数据类型是ndarray,使用ndarray可以处理一维、二维和多维数组,该对象相当于是一个快速而灵活的大数据容器。NumPy 底层代码使用 C 语言编写,解决了 GIL 的限制,ndarray在存取数据的时候,数据与数据的地址都是连续的,这确保了可以进行高效率的批量操作,性能上远远优于 Python 中的list;另一方面ndarray对象提供了更多的方法来处理数据,尤其获取数据统计特征的方法,这些方法也是 Python 原生的list没有的。
准备工作
启动 JupyterLab
jupyter lab
提示:在启动 JupyterLab 之前,建议先安装好数据分析相关依赖项,包括之前提到的三大神器以及相关依赖项。如果使用 Anaconda,则无需单独安装,可以通过 Anaconda 的 Navigator 来启动。
导入
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt说明:如果已经启动了 JupyterLab 但尚未安装相关依赖库,例如尚未安装
numpy,可以在单元格中输入%pip install numpy并运行该单元格来安装 NumPy。当然,我们也可以在单元格中输入%pip install numpy pandas matplotlib把 Python 数据分析三个核心的三方库都安装上。注意上面的代码,我们不仅导入了 NumPy,还将 pandas 和 matplotlib 库一并导入了。
创建数组对象
创建ndarray对象有很多种方法,下面我们介绍一些常用的方法。
方法一:使用array函数,通过list创建数组对象
代码:
array1 = np.array([1, 2, 3, 4, 5])
array1
输出:
array([1, 2, 3, 4, 5])
代码:
array2 = np.array([[1, 2, 3], [4, 5, 6]])
array2
输出:
array([[1, 2, 3],
[4, 5, 6]])
方法二:使用arange函数,指定取值范围和跨度创建数组对象
代码:
array3 = np.arange(0, 20, 2)
array3
输出:
array([ 0, 2, 4, 6, 8, 10, 12, 14, 16, 18])
方法三:使用linspace函数,用指定范围和元素个数创建数组对象,生成等差数列
代码:
array4 = np.linspace(-1, 1, 11)
array4
输出:
array([-1. , -0.8, -0.6, -0.4, -0.2, 0. , 0.2, 0.4, 0.6, 0.8, 1. ])
方法四:使用logspace函数,生成等比数列
代码:
array5 = np.logspace(1, 10, num=10, base=2)
array5
注意:等比数列的起始值是 $\small{2^1}$ ,等比数列的终止值是 $\small{2^{10}}$ ,
num是元素的个数,base就是底数。
输出:
array([ 2., 4., 8., 16., 32., 64., 128., 256., 512., 1024.])
方法五:通过fromstring函数从字符串提取数据创建数组对象
代码:
array6 = np.fromstring('1, 2, 3, 4, 5', sep=',', dtype='i8')
array6
输出:
array([1, 2, 3, 4, 5])
方法六:通过fromiter函数从生成器(迭代器)中获取数据创建数组对象
代码:
def fib(how_many):
a, b = 0, 1
for _ in range(how_many):
a, b = b, a + b
yield a
gen = fib(20)
array7 = np.fromiter(gen, dtype='i8')
array7
输出:
array([ 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,
144, 233, 377, 610, 987, 1597, 2584, 4181, 6765])
方法七:使用numpy.random模块的函数生成随机数创建数组对象
产生 10 个 $\small{[0, 1)}$ 范围的随机小数,代码:
array8 = np.random.rand(10)
array8
输出:
array([0.45556132, 0.67871326, 0.4552213 , 0.96671509, 0.44086463,
0.72650875, 0.79877188, 0.12153022, 0.24762739, 0.6669852 ])
产生 10 个 $\small{[1, 100)}$ 范围的随机整数,代码:
array9 = np.random.randint(1, 100, 10)
array9
输出:
array([29, 97, 87, 47, 39, 19, 71, 32, 79, 34])
产生 20 个 $\small{\mu=50}$ , $\small{\sigma=10}$ 的正态分布随机数,代码:
array10 = np.random.normal(50, 10, 20)
array10
输出:
array([55.04155586, 46.43510797, 20.28371158, 62.67884053, 61.23185964,
38.22682148, 53.17126151, 43.54741592, 36.11268017, 40.94086676,
63.27911699, 46.92688903, 37.1593374 , 67.06525656, 67.47269463,
23.37925889, 31.45312239, 48.34532466, 55.09180924, 47.95702787])
产生 $\small{[0, 1)}$ 范围的随机小数构成的 3 行 4 列的二维数组,代码:
array11 = np.random.rand(3, 4)
array11
输出:
array([[0.54017809, 0.46797771, 0.78291445, 0.79501326],
[0.93973783, 0.21434806, 0.03592874, 0.88838892],
[0.84130479, 0.3566601 , 0.99935473, 0.26353598]])
产生 $\small{[1, 100)}$ 范围的随机整数构成的三维数组,代码:
array12 = np.random.randint(1, 100, (3, 4, 5))
array12
输出:
array([[[94, 26, 49, 24, 43],
[27, 27, 33, 98, 33],
[13, 73, 6, 1, 77],
[54, 32, 51, 86, 59]],
[[62, 75, 62, 29, 87],
[90, 26, 6, 79, 41],
[31, 15, 32, 56, 64],
[37, 84, 61, 71, 71]],
[[45, 24, 78, 77, 41],
[75, 37, 4, 74, 93],
[ 1, 36, 36, 60, 43],
[23, 84, 44, 89, 79]]])
方法八:创建全0、全1或指定元素的数组
使用zeros函数,代码:
array13 = np.zeros((3, 4))
array13
输出:
array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
使用ones函数,代码:
array14 = np.ones((3, 4))
array14
输出:
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
使用full函数,代码:
array15 = np.full((3, 4), 10)
array15
输出:
array([[10, 10, 10, 10],
[10, 10, 10, 10],
[10, 10, 10, 10]])
方法九:使用eye函数创建单位矩阵
代码:
np.eye(4)
输出:
array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]])
方法十:读取图片获得对应的三维数组
代码:
array16 = plt.imread('guido.jpg')
array16
输出:
array([[[ 36, 33, 28],
[ 36, 33, 28],
[ 36, 33, 28],
...,
[ 32, 31, 29],
[ 32, 31, 27],
[ 31, 32, 26]],
[[ 37, 34, 29],
[ 38, 35, 30],
[ 38, 35, 30],
...,
[ 31, 30, 28],
[ 31, 30, 26],
[ 30, 31, 25]],
[[ 38, 35, 30],
[ 38, 35, 30],
[ 38, 35, 30],
...,
[ 30, 29, 27],
[ 30, 29, 25],
[ 29, 30, 25]],
...,
[[239, 178, 123],
[237, 176, 121],
[235, 174, 119],
...,
[ 78, 68, 56],
[ 75, 67, 54],
[ 73, 65, 52]],
[[238, 177, 120],
[236, 175, 118],
[234, 173, 116],
...,
[ 82, 70, 58],
[ 78, 68, 56],
[ 75, 66, 51]],
[[238, 176, 119],
[236, 175, 118],
[234, 173, 116],
...,
[ 84, 70, 61],
[ 81, 69, 57],
[ 79, 67, 53]]], dtype=uint8)
说明:上面的代码读取了当前路径下名为
guido.jpg的图片文件,计算机系统中的图片通常由若干行若干列的像素点构成,而每个像素点又是由红绿蓝三原色构成的,刚好可以用三维数组来表示。读取图片用到了matplotlib库的imread函数。
数组对象的属性
size属性:获取数组元素个数。
代码:
array17 = np.arange(1, 100, 2)
array18 = np.random.rand(3, 4)
print(array16.size)
print(array17.size)
print(array18.size)
输出:
1125000
50
12
shape属性:获取数组的形状。
代码:
print(array16.shape)
print(array17.shape)
print(array18.shape)
输出:
(750, 500, 3)
(50,)
(3, 4)
dtype属性:获取数组元素的数据类型。
代码:
print(array16.dtype)
print(array17.dtype)
print(array18.dtype)
输出:
uint8
int64
float64
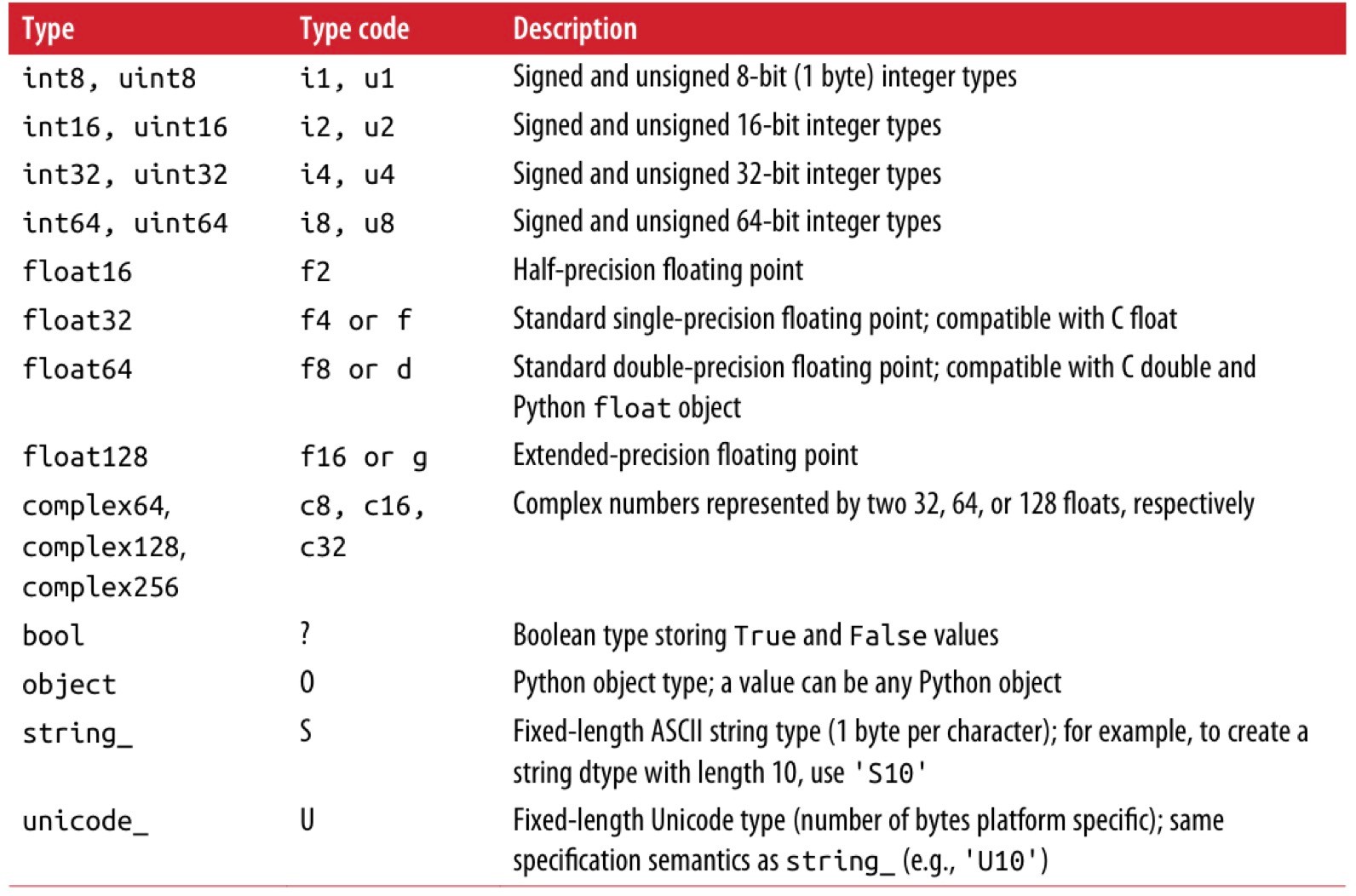
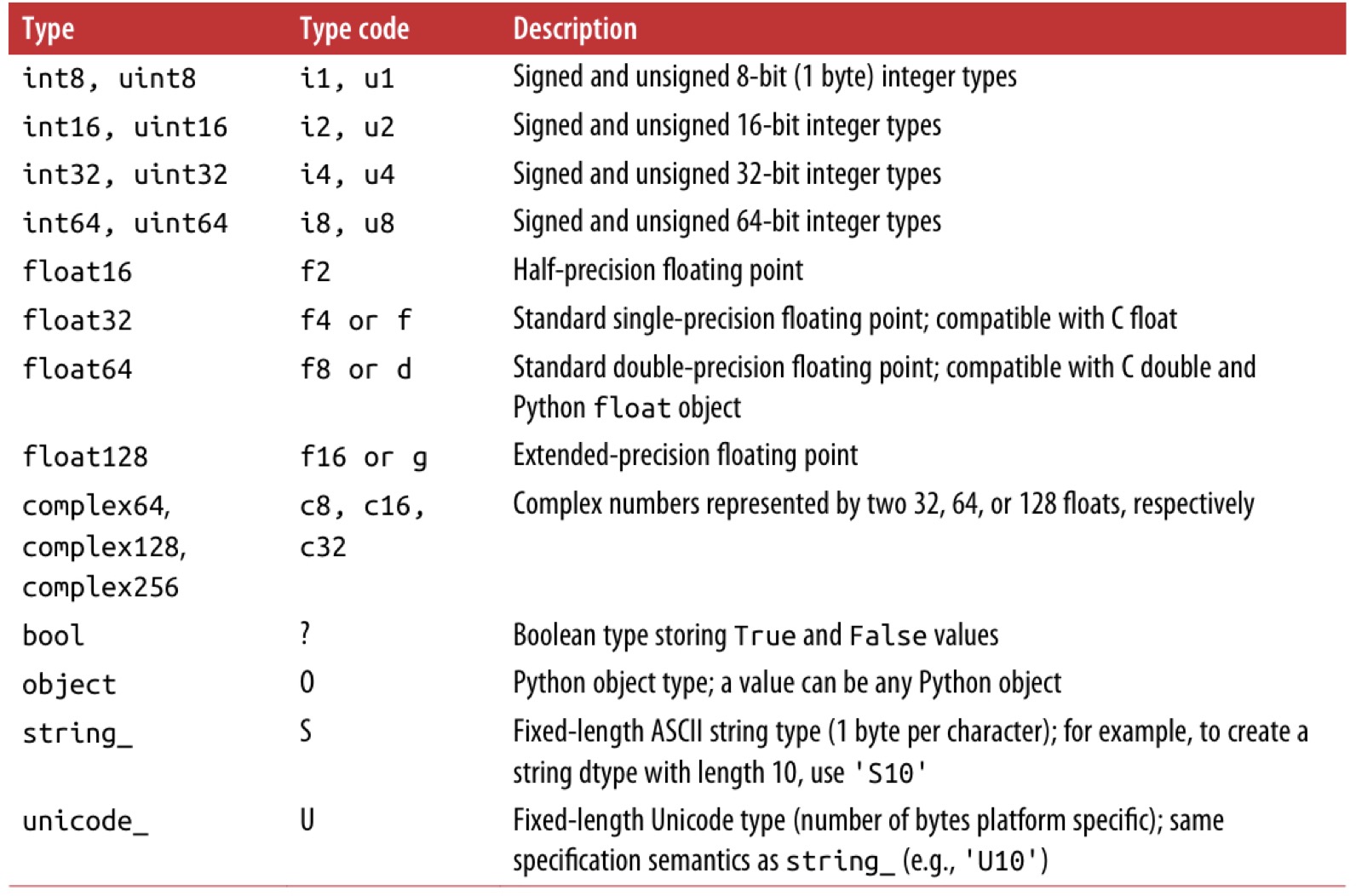
ndarray对象元素的数据类型可以参考如下所示的表格。
ndim属性:获取数组的维度。
代码:
print(array16.ndim)
print(array17.ndim)
print(array18.ndim)
输出:
3
1
2
itemsize属性:获取数组单个元素占用内存空间的字节数。
代码:
print(array16.itemsize)
print(array17.itemsize)
print(array18.itemsize)
输出:
1
8
8
nbytes属性:获取数组所有元素占用内存空间的字节数。
代码:
print(array16.nbytes)
print(array17.nbytes)
print(array18.nbytes)
输出:
1125000
400
96
数组的索引运算
和 Python 中的列表类似,NumPy 的ndarray对象可以进行索引和切片操作,通过索引可以获取或修改数组中的元素,通过切片操作可以取出数组的一部分,我们把切片操作也称为切片索引。
普通索引
类似于 Python 中list类型的索引运算。
代码:
array19 = np.arange(1, 10)
print(array19[0], array19[array19.size - 1])
print(array19[-array20.size], array19[-1])
输出:
1 9
1 9
代码:
array20 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
array20[2]
输出:
array([7, 8, 9])
代码:
print(array20[0][0])
print(array20[-1][-1])
输出:
1
9
代码:
print(array20[1][1])
print(array20[1, 1])
输出:
5
5
代码:
array20[1][1] = 10
array20
输出:
array([[ 1, 2, 3],
[ 4, 10, 6],
[ 7, 8, 9]])
代码:
array20[1] = [10, 11, 12]
array20
输出:
array([[ 1, 2, 3],
[10, 11, 12],
[ 7, 8, 9]])
切片索引
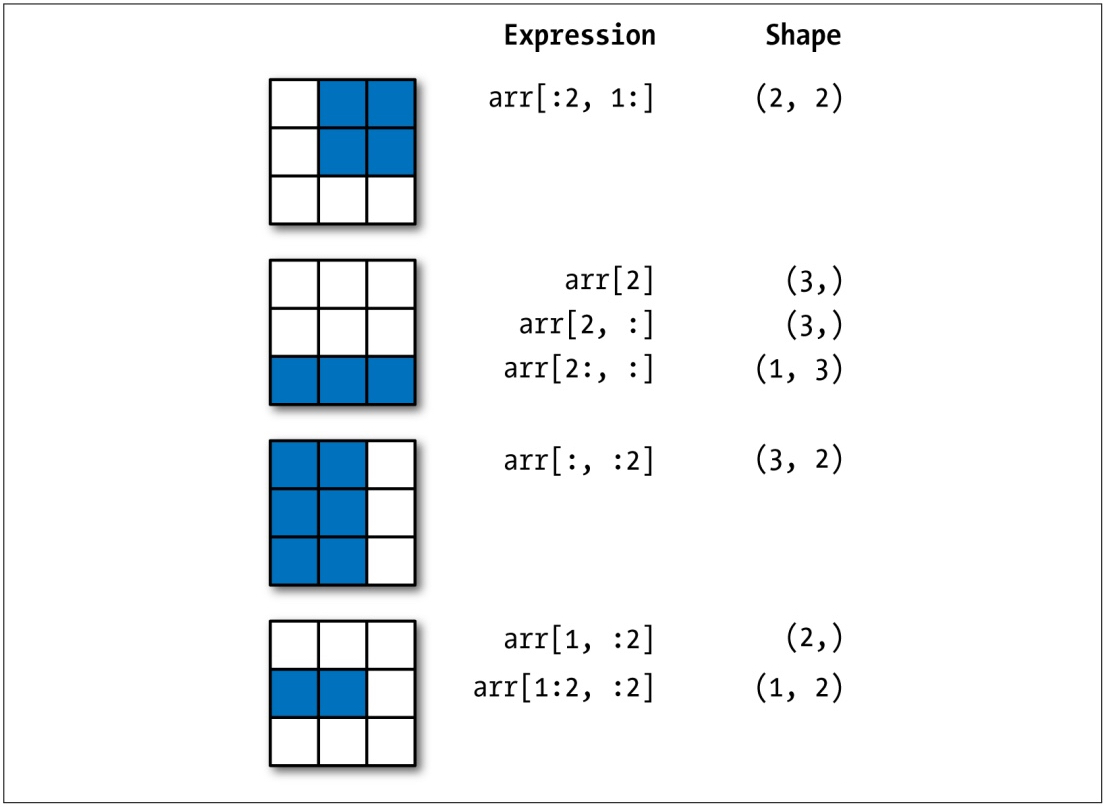
切片索引是形如[开始索引:结束索引:跨度]的语法,通过指定开始索引(默认值无穷小)、结束索引(默认值无穷大)和跨度(默认值1),从数组中取出指定部分的元素并构成新的数组。因为开始索引、结束索引和步长都有默认值,所以它们都可以省略,如果不指定步长,第二个冒号也可以省略。一维数组的切片运算跟 Python 中的list类型的切片非常类似,此处不再赘述,二维数组的切片可以参考下面的代码,相信非常容易理解。
代码:
array20[:2, 1:]
输出:
array([[ 2, 3],
[11, 12]])
代码:
array20[2, :]
输出:
array([7, 8, 9])
代码:
array20[2:, :]
输出:
array([[7, 8, 9]])
代码:
array20[:, :2]
输出:
array([[ 1, 2],
[10, 11],
[ 7, 8]])
代码:
array20[::2, ::2]
输出:
array([[1, 3],
[7, 9]])
代码:
array20[::-2, ::-2]
输出:
array([[9, 7],
[3, 1]])
关于数组的索引和切片运算,大家可以通过下面的两张图来增强印象,这两张图来自《利用Python进行数据分析》一书,它是 pandas 库的作者 Wes McKinney 撰写的 Python 数据分析领域的经典教科书,有兴趣的读者可以购买和阅读原书。
图1:二维数组的普通索引
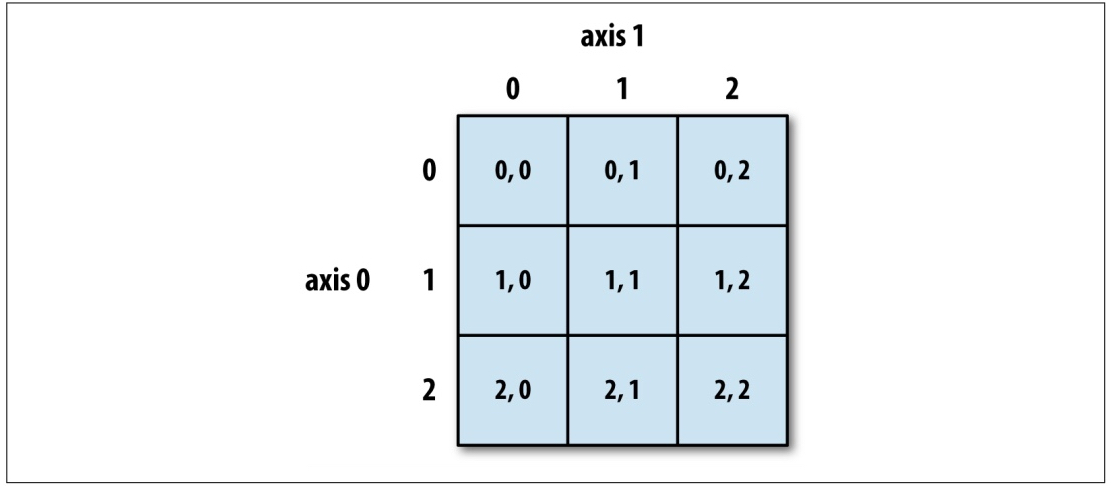
图2:二维数组的切片索引
花式索引
花式索引是用保存整数的数组充当一个数组的索引,这里所说的数组可以是 NumPy 的ndarray,也可以是 Python 中list、tuple等可迭代类型,可以使用正向或负向索引。
代码:
array19[[0, 1, 1, -1, 4, -1]]
输出:
array([1, 2, 2, 9, 5, 9])
代码:
array20[[0, 2]]
输出:
array([[1, 2, 3],
[7, 8, 9]])
代码:
array20[[0, 2], [1, 2]]
输出:
array([2, 9])
代码:
array20[[0, 2], 1]
输出:
array([2, 8])
布尔索引
布尔索引就是通过保存布尔值的数组充当一个数组的索引,布尔值为True的元素保留,布尔值为False的元素不会被选中。布尔值的数组可以手动构造,也可以通过关系运算来产生。
代码:
array19[[True, True, False, False, True, False, False, True, True]]
输出:
array([1, 2, 5, 8, 9])
代码:
array19 > 5
输出:
array([False, False, False, False, False, True, True, True, True])
代码:
~(array19 > 5)
输出:
array([ True, True, True, True, True, False, False, False, False])
说明:
~运算符可以对布尔数组中的布尔值进行逻辑取反,也就是原来的True会变成False,原来的False会变成True。
代码:
array19[array19 > 5]
输出:
array([6, 7, 8, 9])
代码:
array19 % 2 == 0
输出:
array([False, True, False, True, False, True, False, True, False])
代码:
array19[array19 % 2 == 0]
输出:
array([2, 4, 6, 8])
代码:
(array19 > 5) & (array19 % 2 == 0)
输出:
array([False, False, False, False, False, True, False, True, False])
说明:
&运算符可以作用于两个布尔数组,如果两个数组对应元素都是True,那么运算的结果就是True,否则就是False,该运算符的运算规则类似于 Python 中的and运算符,只不过作用的对象是两个布尔数组。
代码:
array19[(array19 > 5) & (array19 % 2 == 0)]
输出:
array([6, 8])
代码:
array19[(array19 > 5) | (array19 % 2 == 0)]
输出:
array([2, 4, 6, 7, 8, 9])
说明:
|运算符可以作用于两个布尔数组,如果两个数组对应元素都是False,那么运算的结果就是False,否则就是True,该运算符的运算规则类似于 Python 中的or运算符,只不过作用的对象是两个布尔数组。
代码:
array20[array21 % 2 != 0]
输出:
array([1, 3, 5, 7, 9])
关于索引运算需要说明的是,切片索引虽然创建了新的数组对象,但是新数组和原数组共享了数组中的数据,简单的说,无论你通过新数组对象或原数组对象修改数组中的数据,修改的其实是内存中的同一块数据。花式索引和布尔索引也会创建新的数组对象,而且新数组复制了原数组的元素,新数组和原数组并不是共享数据的关系,这一点可以查看数组对象的base属性,有兴趣的读者可以自行探索。
案例:通过数组切片处理图像
学习基础知识总是比较枯燥且没有成就感的,所以我们还是来个案例为大家演示下上面学习的数组索引和切片操作到底有什么用。前面我们说到过,可以用三维数组来表示图像,那么通过图像对应的三维数组进行操作,就可以实现对图像的处理,如下所示。
读入图片创建三维数组对象。
guido_image = plt.imread('guido.jpg')
plt.imshow(guido_image)

对数组的0轴进行反向切片,实现图像的垂直翻转。
plt.imshow(guido_image[::-1])

对数组的1轴进行反向切片,实现图像的水平翻转。
plt.imshow(guido_image[:,::-1])

通过切片操作实现抠图,将吉多大叔的头抠出来。
plt.imshow(guido_image[30:350, 90:300])

通过切片操作实现降采样。
plt.imshow(guido_image[::10, ::10])

数组对象的方法
获取描述统计信息
描述统计信息主要包括数据的集中趋势、离散程度和频数分析等,其中集中趋势主要看均值和中位数,离散程度可以看极值、方差、标准差等,详细的内容大家可以阅读《统计思维系列课程01:解读数据》。
array1 = np.random.randint(1, 100, 10)
array1
输出:
array([46, 51, 15, 42, 53, 71, 20, 62, 6, 94])
计算总和、均值和中位数。
代码:
print(array1.sum())
print(np.sum(array1))
print(array1.mean())
print(np.mean(array1))
print(np.median(array1))
print(np.quantile(array1, 0.5))
说明:上面代码中的
mean、median和quantile分别是 NumPy 中计算算术平均值、中位数和分位数的函数,其中quantitle函数的第二个参数设置为0.5表示计算50%分位数,也就是中位数。
输出:
460
460
46.0
46.0
48.5
48.5
极值、全距和四分位距离。
代码:
print(array1.max())
print(np.amax(array1))
print(array1.min())
print(np.amin(array1))
print(np.ptp(array1))
print(np.ptp(array1))
q1, q3 = np.quantile(array1, [0.25, 0.75])
print(q3 - q1)
输出:
94
94
6
6
88
88
34.25
方差、标准差和变异系数。
代码:
print(array1.var())
print(np.var(array1))
print(array1.std())
print(np.std(array1))
print(array1.std() / array1.mean())
输出:
651.2
651.2
25.51862065237853
25.51862065237853
0.5547526228777941
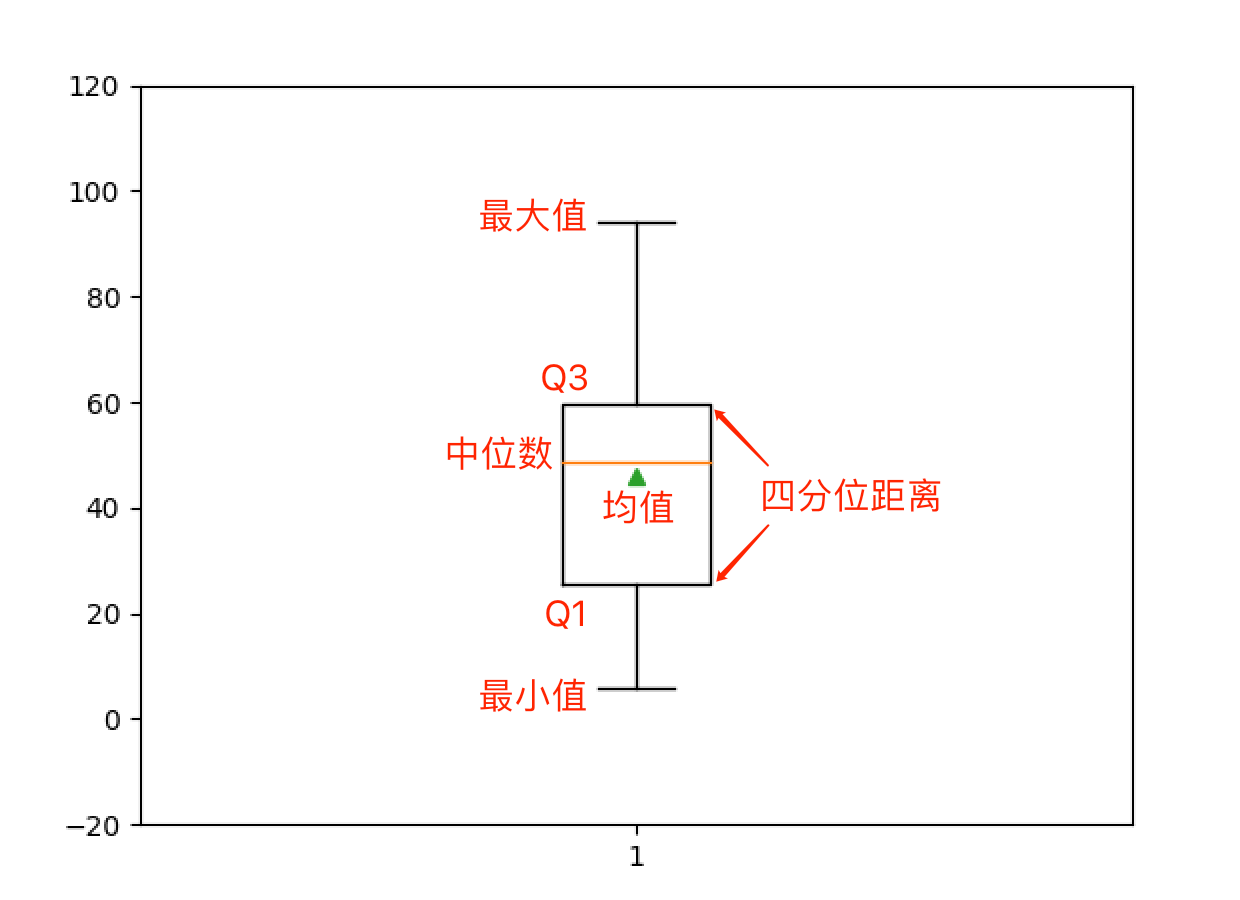
绘制箱线图。
箱线图又称为盒须图,是显示一组数据分散情况的统计图,因形状如箱子而得名。 它主要用于反映原始数据分布的特征,还可以进行多组数据分布特征的比较。
代码:
plt.boxplot(array1, showmeans=True)
plt.ylim([-20, 120])
plt.show()
输出:
值得注意的是,对于二维或更高维的数组,在获取描述统计信息时,可以通过名为axis的参数指定均值、方差等运算是沿着哪一个轴来执行,axis参数不同,执行的结果可能是大相径庭的,如下所示。
代码:
array2 = np.random.randint(60, 101, (5, 3))
array2
输出:
array([[72, 64, 73],
[61, 73, 61],
[76, 85, 77],
[97, 88, 90],
[63, 93, 82]])
代码:
array2.mean()
输出:
77.0
代码:
array2.mean(axis=0)
输出:
array([73.8, 80.6, 76.6])
代码:
array2.mean(axis=1)
输出:
array([69.66666667, 65. , 79.33333333, 91.66666667, 79.33333333])
代码:
array2.max(axis=0)
输出:
array([97, 93, 90])
代码:
array2.max(axis=1)
输出:
array([73, 73, 85, 97, 93])
再看看绘制箱线图,对于二维数组每一列都会产生一个统计图形,如下所示。
代码:
plt.boxplot(array2, showmeans=True)
plt.ylim([-20, 120])
plt.show()
输出:
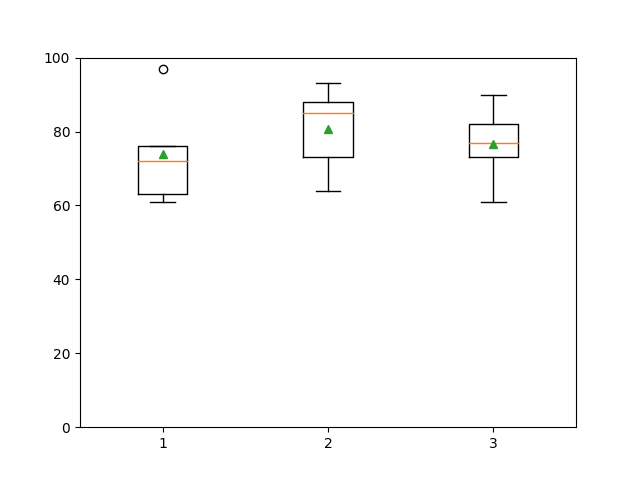
说明:箱线图中的小圆圈用来表示离群点,也就是大于 $\small{Q_3 + 1.5 \times IQR}$ 或小于 $\small{Q_1 - 1.5 \times IQR}$ 的值。公式中的常量 1.5 可以通过绘制箱线图的
boxplot函数的whis参数进行修改,常用的值是 1.5 和 3,修改为 3 通常是为了标识出极度离群点。
需要说明的是,NumPy 的数组对象并没有提供计算几何平均值、调和平均值、去尾平均值等的方法,如果有这方面的需求,可以使用名为 scipy 的三方库,它的stats模块中提供了这些函数。此外,该模块还提供了计算众数、变异系数、偏态、峰度的函数,代码如下所示。
代码:
from scipy import stats
print(np.mean(array1)) # 算术平均值
print(stats.gmean(array1)) # 几何平均值
print(stats.hmean(array1)) # 调和平均值
print(stats.tmean(array1, [10, 90])) # 去尾平均值
print(stats.variation(array1)) # 变异系数
print(stats.skew(array1)) # 偏态系数
print(stats.kurtosis(array1)) # 峰度系数
输出:
46.0
36.22349548825599
24.497219530825497
45.0
0.5547526228777941
0.11644192634527782
-0.7106251396024126
其他相关方法概述
all()/any()方法:判断数组是否所有元素都是True/ 判断数组是否有为True的元素。astype()方法:拷贝数组,并将数组中的元素转换为指定的类型。reshape()方法:调整数组对象的形状。dump()方法:保存数组到二进制文件中,可以通过 NumPy 中的load()函数从保存的文件中加载数据创建数组。代码:
array.dump('array1-data')
array3 = np.load('array1-data', allow_pickle=True)
array3输出:
array([46, 51, 15, 42, 53, 71, 20, 62, 6, 94])
tofile()方法:将数组对象写入文件中。array1.tofile('array.txt', sep=',')fill()方法:向数组中填充指定的元素。flatten()方法:将多维数组扁平化为一维数组。代码:
array2.flatten()
输出:
array([1, 2, 3, 4, 5, 6, 7, 8, 9])
nonzero()方法:返回非0元素的索引。round()方法:对数组中的元素做四舍五入操作。sort()方法:对数组进行就地排序。代码:
array1.sort()
array1输出:
array([ 6, 15, 20, 42, 46, 51, 53, 62, 71, 94])
swapaxes()和transpose()方法:交换数组指定的轴和转置。代码:
array2.swapaxes(0, 1)
输出:
array([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])代码:
array2.transpose()
输出:
array([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])tolist()方法:将数组转成 Python 中的list。代码:
print(array2.tolist())
print(type(array2.tolist()))输出:
[[1, 2, 3], [4, 5, 6], [7, 8, 9]]
<class 'list'>
数组的运算
使用 NumPy 最为方便的是当需要对数组元素进行运算时,不用编写循环代码遍历每个元素,所有的运算都会自动的矢量化。简单的说就是,NumPy 中的数学运算和数学函数会自动作用于数组中的每个成员。
数组跟标量的运算
NumPy 的数组可以跟一个数值进行加、减、乘、除、求模、求幂等运算,对应的运算会作用到数组的每一个元素上,如下所示。
代码:
array1 = np.arange(1, 10)
print(array1 + 10)
print(array1 * 10)
输出:
[11 12 13 14 15 16 17 18 19]
[10 20 30 40 50 60 70 80 90]
除了上述的运算,关系运算也是没有问题的,之前讲布尔索引的时候已经遇到过了。
代码:
print(array1 > 5)
print(array1 % 2 == 0)
输出:
[False False False False False True True True True]
[False True False True False True False True False]
数组跟数组的运算
NumPy 的数组跟数组也可以执行算术运算和关系运算,运算会作用于两个数组对应的元素上,这就要求两个数组的形状(shape属性)要相同,如下所示。
代码:
array2 = np.array([1, 1, 1, 2, 2, 2, 3, 3, 3])
print(array1 + array2)
print(array1 * array2)
print(array1 ** array2)
输出:
[ 2 3 4 6 7 8 10 11 12]
[ 1 2 3 8 10 12 21 24 27]
[ 1 2 3 16 25 36 343 512 729]
代码:
print(array1 > array2)
print(array1 % array2 == 0)
输出:
[False True True True True True True True True]
[ True True True True False True False False True]
通用一元函数
NumPy 中通用一元函数的参数是一个数组对象,函数会对数组进行元素级的处理,例如:sqrt函数会对数组中的每个元素计算平方根,而log2函数会对数组中的每个元素计算以2为底的对数,代码如下所示。
代码:
print(np.sqrt(array1)) print(np.log2(array1))
输出:
[1. 1.41421356 1.73205081 2. 2.23606798 2.44948974 2.64575131 2.82842712 3. ] [0. 1. 1.5849625 2. 2.32192809 2.5849625 2.80735492 3. 3.169925 ]
表1:通用一元函数
| 函数 | 说明 |
|---|---|
abs / fabs | 求绝对值的函数 |
sqrt | 求平方根的函数,相当于array ** 0.5 |
square | 求平方的函数,相当于array ** 2 |
exp | 计算 $\small{e^x}$ 的函数 |
log / log10 / log2 | 对数函数(e为底 / 10为底 / 2为底) |
sign | 符号函数(1 - 正数;0 - 零;-1 - 负数) |
ceil / floor | 上取整 / 下取整 |
isnan | 返回布尔数组,NaN对应True,非NaN对应False |
isfinite / isinf | 判断数值是否为无穷大的函数 |
cos / cosh / sin | 三角函数 |
sinh / tan / tanh | 三角函数 |
arccos / arccosh / arcsin | 反三角函数 |
arcsinh / arctan / arctanh | 反三角函数 |
rint / round | 四舍五入函数 |
通用二元函数
NumPy 中通用二元函数的参数是两个数组对象,函数会对两个数组中的对应元素进行运算,例如:maximum函数会对两个数组中对应的元素找最大值,而power函数会对两个数组中对应的元素进行求幂操作,代码如下所示。
代码:
array3 = np.array([[4, 5, 6], [7, 8, 9]]) array4 = np.array([[1, 2, 3], [3, 2, 1]]) print(np.maximum(array3, array4)) print(np.power(array3, array4))
输出:
[[4 5 6] [7 8 9]] [[ 4 25 216] [343 64 9]]
表2:通用二元函数
| 函数 | 说明 |
|---|---|
add(x, y) / substract(x, y) | 加法函数 / 减法函数 |
multiply(x, y) / divide(x, y) | 乘法函数 / 除法函数 |
floor_divide(x, y) / mod(x, y) | 整除函数 / 求模函数 |
allclose(x, y) | 检查数组x和y元素是否几乎相等 |
power(x, y) | 数组x的元素 $\small{x{i}}$ 和数组y的元素 $\small{y{i}}$,计算 $\small{x{i}^{y{i}}}$ |
maximum(x, y) / fmax(x, y) | 两两比较元素获取最大值 / 获取最大值(忽略NaN) |
minimum(x, y) / fmin(x, y) | 两两比较元素获取最小值 / 获取最小值(忽略NaN) |
dot(x, y) | 点积运算(数量积,通常记为 $\small{\cdot}$ ,用于欧几里得空间(Euclidean space)) |
inner(x, y) | 内积运算(内积的含义要高于点积,点积相当于是内积在欧几里得空间 $\small{\mathbb{R}^{n}}$ 的特例,而内积可以推广到赋范向量空间,只要它满足平行四边形法则即可) |
cross(x, y) | 叉积运算(向量积,通常记为 $\small{\times}$ ,运算结果是一个向量) |
outer(x, y) | 外积运算(张量积,通常记为 $\small{\bigotimes}$ ,运算结果通常是一个矩阵) |
intersect1d(x, y) | 计算x和y的交集,返回这些元素构成的有序数组 |
union1d(x, y) | 计算x和y的并集,返回这些元素构成的有序数组 |
in1d(x, y) | 返回由判断x 的元素是否在y中得到的布尔值构成的数组 |
setdiff1d(x, y) | 计算x和y的差集,返回这些元素构成的数组 |
setxor1d(x, y) | 计算x和y的对称差,返回这些元素构成的数组 |
说明:关于向量和矩阵的运算,我们在下一个章节加以说明。
广播机制
上面数组运算的例子中,两个数组的形状(shape属性)是完全相同的,我们再来研究一下,两个形状不同的数组是否可以直接做二元运算或使用通用二元函数进行运算,请看下面的例子。
代码:
array5 = np.array([[0, 0, 0], [1, 1, 1], [2, 2, 2], [3, 3, 3]]) array6 = np.array([1, 2, 3]) array5 + array6
输出:
array([[1, 2, 3], [2, 3, 4], [3, 4, 5], [4, 5, 6]])
代码:
array7 = np.array([[1], [2], [3], [4]]) array5 + array7
输出:
array([[1, 1, 1], [3, 3, 3], [5, 5, 5], [7, 7, 7]])
通过上面的例子,我们发现形状不同的数组仍然有机会进行二元运算,但这不代表任意形状的数组都可以进行二元运算。简单的说,只有两个数组后缘维度相同或者后缘维度不同但其中一个数组后缘维度为1时,广播机制才会被触发。通过广播机制,NumPy 将两个原本形状不相同的数组变成形状相同,才能进行二元运算。所谓后缘维度,指的是数组形状(shape属性)从后往前看对应的部分,我们举例说明。
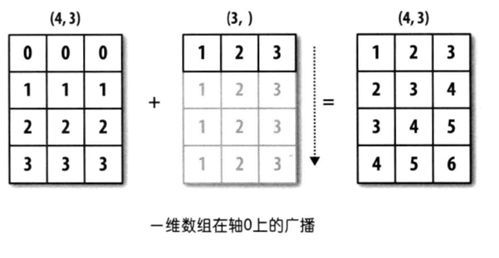
上图中,一个数组的形状是(4, 3),另一个数组的形状是(3, ),从后往前看对应的部分都是3,属于后缘维度相同,可以应用广播机制,第二个数组会沿着缺失元素那个轴的方向去广播自己,最终让两个数组形状达成一致。
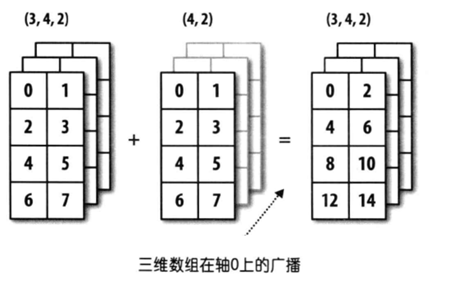
上图中,一个数组的形状是(3, 4, 2),另一个数组的形状是(4, 2),从后往前看对应的部分都是(4, 2),属于后缘维度相同,可以应用广播机制,第二个数组会沿着缺失元素那个轴的方向去广播自己,最终让两个数组形状达成一致。
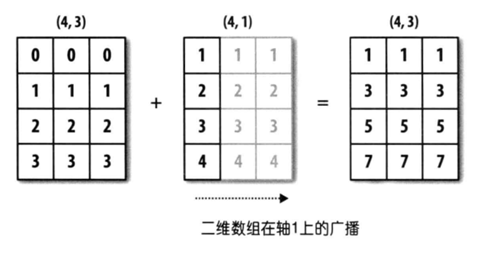
上图中,一个数组的形状是(4, 3),另一个数组的形状是(4, 1),这是后缘维度不相同的情况,但是第二个数组跟第一个数组不同的地方为1,第二个数组可以沿着为1 的那个轴广播自己,最终让两个数组形状达成一致。
思考:一个3行1列的二维数组和一个1行3列的二维数组能够执行加法运算吗?
其他常用函数
除了上面讲到的函数外,NumPy 中还提供了很多用于处理数组的函数,ndarray对象的很多方法也可以通过调用函数来实现,下表给出了一些常用的函数。
表3:NumPy其他常用函数
| 函数 | 说明 |
|---|---|
unique | 去除数组重复元素,返回唯一元素构成的有序数组 |
copy | 返回拷贝数组得到的数组 |
sort | 返回数组元素排序后的拷贝 |
split / hsplit / vsplit | 将数组拆成若干个子数组 |
stack / hstack / vstack | 将多个数组堆叠成新数组 |
concatenate | 沿着指定的轴连接多个数组构成新数组 |
append / insert | 向数组末尾追加元素 / 在数组指定位置插入元素 |
argwhere | 找出数组中非0元素的位置 |
extract / select / where | 按照指定的条件从数组中抽取或处理数组元素 |
flip | 沿指定的轴翻转数组中的元素 |
fromregex | 通过读取文件和正则表达式解析获取数据创建数组对象 |
repeat / tile | 通过对元素的重复来创建新数组 |
roll | 沿指定轴对数组元素进行移位 |
resize | 重新调整数组的大小 |
place / put | 将数组中满足条件的元素/指定的元素替换为指定的值 |
partition | 用选定的元素对数组进行一次划分并返回划分后的数组 |
去重(重复元素只保留一项)。
代码:
np.unique(array5)
输出:
array([0, 1, 2, 3])
堆叠和拼接。
代码:
array8 = np.array([[1, 1, 1], [2, 2, 2], [3, 3, 3]]) array9 = np.array([[4, 4, 4], [5, 5, 5], [6, 6, 6]]) np.hstack((array8, array9))
输出:
array([[1, 1, 1, 4, 4, 4], [2, 2, 2, 5, 5, 5], [3, 3, 3, 6, 6, 6]])
代码:
np.vstack((array8, array9))
输出:
array([[1, 1, 1], [2, 2, 2], [3, 3, 3], [4, 4, 4], [5, 5, 5], [6, 6, 6]])
代码:
np.concatenate((array8, array9))
输出:
array([[1, 1, 1], [2, 2, 2], [3, 3, 3], [4, 4, 4], [5, 5, 5], [6, 6, 6]])
代码:
np.concatenate((array8, array9), axis=1)
输出:
array([[1, 1, 1, 4, 4, 4], [2, 2, 2, 5, 5, 5], [3, 3, 3, 6, 6, 6]])
追加和插入元素。
代码:
np.append(array1, [10, 100])
输出:
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 100])
代码:
np.insert(array1, 1, [98, 99, 100])
输出:
array([ 1, 98, 99, 100, 2, 3, 4, 5, 6, 7, 8, 9])
抽取和处理元素。
代码:
np.extract(array1 % 2 != 0, array1)
输出:
array([1, 3, 5, 7, 9])
说明:上面
extract函数的操作相当于我们之前讲的布尔索引。
代码:
np.select([array1 <= 3, array1 >= 7], [array1 * 10, array1 ** 2])
输出:
array([10, 20, 30, 0, 0, 0, 49, 64, 81])
说明:上面
select函数的第一个参数设置了两个条件,满足第一个条件的元素执行了乘以10的操作,满足第二个条件的元素执行了求平方的操作,两个条件都不能满足的数组元素会被处理为0。
代码:
np.where(array1 <= 5, array1 * 10, array1 ** 2)
输出:
array([10, 20, 30, 40, 50, 36, 49, 64, 81])
说明:上面
where函数的第一个参数给出了条件,满足条件的元素执行了乘以10的操作,不能满足条件的元素执行了求平方的操作。
重复数组元素创建新数组。
代码:
np.repeat(array1, 3)
输出:
array([1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 7, 7, 7, 8, 8, 8, 9, 9, 9])
代码:
np.tile(array1, 2)
输出:
array([1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, 7, 8, 9])
调整数组大小。
代码:
np.resize(array1, (5, 3))
输出:
array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [1, 2, 3], [4, 5, 6]])
提示:
array1原本是一个有9个元素的一维数组,通过resize函数调整成为5行3列共15个元素的二维数组,缺少的元素通过复用原数组中的元素来补充。
代码:
np.resize(array5, (2, 4))
输出:
array([[0, 0, 0, 1], [1, 1, 2, 2]])
替换数组元素。
代码:
np.put(array1, [0, 1, -1, 3, 5], [100, 200]) array1
输出:
array([100, 200, 3, 200, 5, 100, 7, 8, 100])
说明:上面
put函的第二个参数给出了要被替换的元素的索引,但是用来作为替换值的元素只有100和200,所以这两个值会被循环使用,因此索引为0、1、-1、3、5的元素被依次替换成了100、200、100、200、100。
代码:
np.place(array1, array1 > 5, [1, 2, 3]) array1
输出:
array([1, 2, 3, 3, 5, 1, 2, 3, 1])
注意:
put函数和place函数都没有返回新的数组对象,而是在原来的数组上直接进行替换。
向量
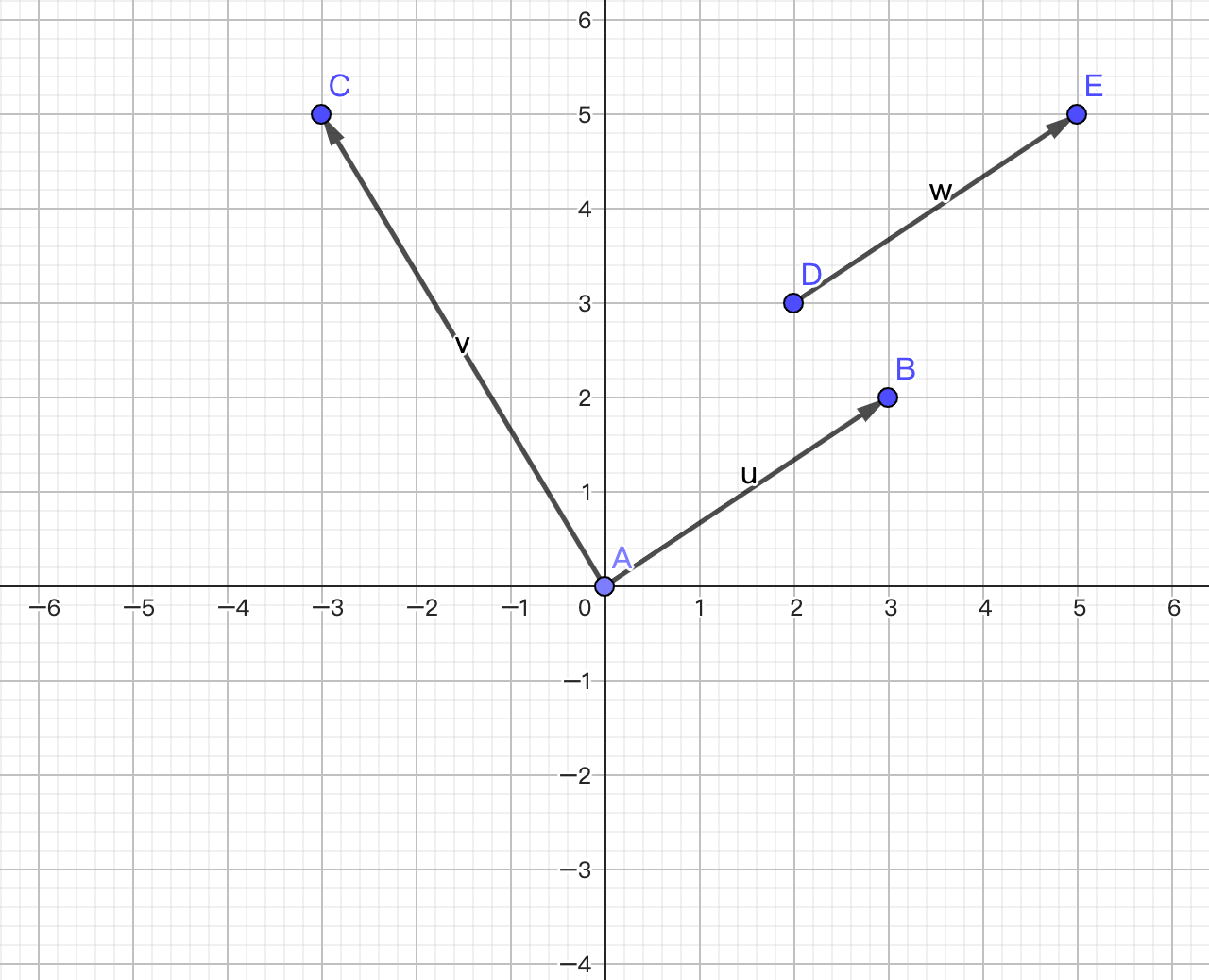
向量(vector)也叫矢量,是一个同时具有大小和方向,且满足平行四边形法则的几何对象。与向量相对的概念叫标量或数量,标量只有大小,绝大多数情况下没有方向。我们通常用带箭头的线段来表示向量,在平面直角坐标系中的向量如下图所示。需要注意的是,向量是表达大小和方向的量,并没有规定起点和终点,所以相同的向量可以画在任意位置,例如下图中 $\small{\boldsymbol{w}}$ 和 $\small{\boldsymbol{u}}$ 两个向量并没有什么区别。
向量有很多种代数表示法,对于二维空间的向量,下面几种写法都是可以的。
向量的大小称为向量的模,它是一个标量,对于二维空间的向量,模可以通过下面的公式计算。
注意,这里的 $\small{\lvert \boldsymbol{a} \rvert}$ 并不是绝对值,你可以将其称为向量 $\small{\boldsymbol{a}}$ 的二范数,这是数学中的符号重用现象。上面的写法和概念也可以推广到 $\small{n}$ 维空间,我们通常用 表示 $\small{n}$ 维空间,我们刚才说的二维空间可以记为
,三维空间可以记为
。虽然生活在三维空间的我们很难想象四维空间、五维空间是什么样子,但是这并不影响我们探讨高维空间,机器学习中,我们经常把有
个特征的训练样本称为一个
维向量。
向量的加法
相同维度的向量可以相加得到一个新的向量,运算的方法是将向量的每个分量相加,如下所示。
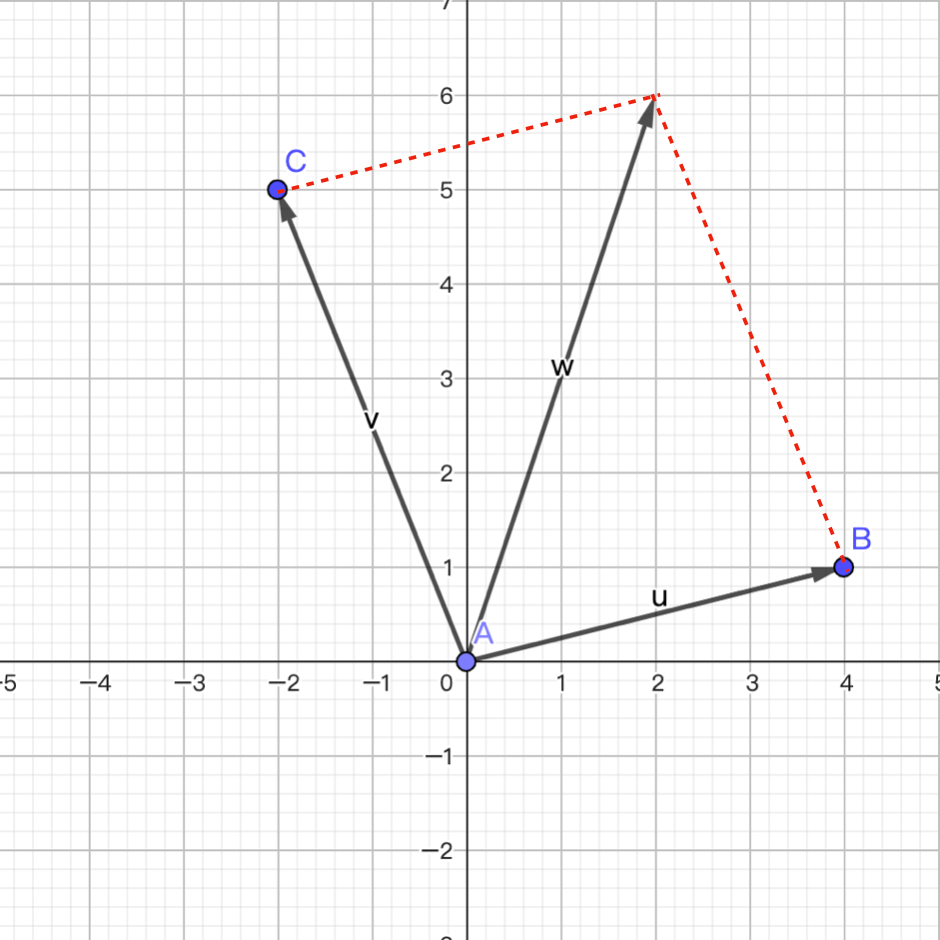
向量的加法满足“平行四边形法则”,即两个向量 $\small{\boldsymbol{u}}$ 和 $\small{\boldsymbol{v}}$ 构成了平行四边形的两条邻边,相加的结果是平行四边形的对角线,如下图所示。
向量的数乘
一个向量 $\small{\boldsymbol{v}}$ 可以和一个标量 $\small{k}$ 相乘,运算的方法是将向量中的每个分量与该标量相乘即可,如下所示。
我们可以用 NumPy 的数组来表示向量,向量的加法可以通过两个数组的加法来实现,向量的数乘可以通过数组和标量的乘法来实现,此处不再进行赘述。
向量的点积
点积(dot product)是两个向量之间最为重要的运算之一,运算的方法是将两个向量对应分量的乘积求和,所以点积的结果是一个标量,其几何意义是两个向量的模乘以二者夹角的余弦如下所示。
假如我们用三维向量来表示用户对喜剧片、言情片和动作片这三类电影的偏好,我们用 1 到 5 的数字来表示喜欢的程度,其中 5 表示非常喜欢,4 表示比较喜欢,3 表示无感,2 表示比较反感,1 表示特别反感。那么,下面的向量表示用户非常喜欢喜剧片,特别反感言情片,对动作片不喜欢也不反感。
现在有两部电影上映了,一部属于言情喜剧片,一部属于喜剧动作片,我们把两部电影也通过3维向量的方式进行表示,如下所示。
如果现在我们需要向刚才的用户推荐一部电影,我们应该给他推荐哪一部呢?我们可以将代表用户的向量 和代表电影的向量
和
分别进行点积运算,再除以向量的模长,得到向量夹角的余弦值,余弦值越接近 1,说明向量的夹角越接近 0 度,也就是两个向量的相似度越高。很显然,我们应该向用户推荐跟他观影喜好相似度更高的电影。
大家可能会说,向量 代表的电影肉眼可见跟用户是更加匹配的。的确,对于一个三维向量我们凭借直觉也能够给出正确的答案,但是对于一个
维向量,当
的值非常大时,你还有信心凭借肉眼的观察和本能的直觉给出准确的答案吗?向量的点积可以通过
dot函数来计算,而向量的模长可以通过 NumPy 的linalg模块中的norm函数来计算,代码如下所示。
u = np.array([5, 1, 3])
m1 = np.array([4, 5, 1])
m2 = np.array([5, 1, 5])
print(np.dot(u, m1) / (np.linalg.norm(u) * np.linalg.norm(m1))) # 0.7302967433402214
print(np.dot(u, m2) / (np.linalg.norm(u) * np.linalg.norm(m2))) # 0.9704311900788593
向量的叉积
在二维空间,两个向量的叉积是这样定义的:
对于三维空间,两个向量的叉积结果是一个向量,如下所示:
因为叉积的结果是向量,所以 和
的结果并不相同,事实上:
NumPy 中可以通过cross函数来计算向量的叉积,代码如下所示。
print(np.cross(u, m1)) # [-14 7 21]
print(np.cross(m1, u)) # [ 14 -7 -21]
行列式
行列式(determinant)通常记作 或
,其中
是一个
阶方阵。行列式可以看做是有向面积或体积的概念在一般欧几里得空间的推广,或者说行列式描述的是一个线性变换对“体积”所造成的影响。行列式的概念最早出现在解线性方程组的过程中,十七世纪晚期,关孝和(日本江户时代的数学家)与莱布尼茨的著作中已经使用行列式来确定线性方程组解的个数以及形式;十八世纪开始,行列式开始作为独立的数学概念被研究;十九世纪以后,行列式理论进一步得到发展和完善。
行列式的性质
行列式是由向量引出的,所以行列式解释的其实是向量的性质。
性质1:如果 中某行(或某列)的元素全部为 0,那么
。
性质2:如果 中某行(或某列)有公共因子
,则可以提出
,得到行列式
,且
。
性质3:如果 中某行(或某列)的每个元素是两数之和,则此行列式可拆分为两个行列式相加,如下所示。
性质4:如果中两行(或两列)元素对应成比例,那么
。
性质5:如果 中两行(或两列)互换得到
,那么
。
性质6:将 中某行(或某列)的
倍加进另一行(或另一列)里,行列式的值不变,如下所示。
性质7:将行列式的行列互换,行列式的值不变,如下所示。
性质8:方块矩阵 和
的乘积的行列式等于其行列式的乘积,即
。特别的,若将矩阵中的每一行都乘以常数
,那么行列式的值将是原来的
倍,即
,其中
是
阶单位矩阵。
性质9:若 是可逆矩阵,那么
。
行列式的计算
$\small{n}$ 阶行列式的计算公式如下所示:
对于二阶行列式,上面的公式相当于:
对于三阶行列式,上面的计算公式相当于:
高阶行列式可以用代数余子式(cofactor)展开成多个低阶行列式,如下所示:
其中, 是原行列式去掉
所在行和列之后剩余的部分构成的行列式,以此类推。
矩阵
矩阵(matrix)是由一系列元素排成的矩形阵列,矩阵里的元素可以是数字、符号或数学公式。矩阵可以进行加法、减法、数乘、转置、矩阵乘法等运算,如下图所示。

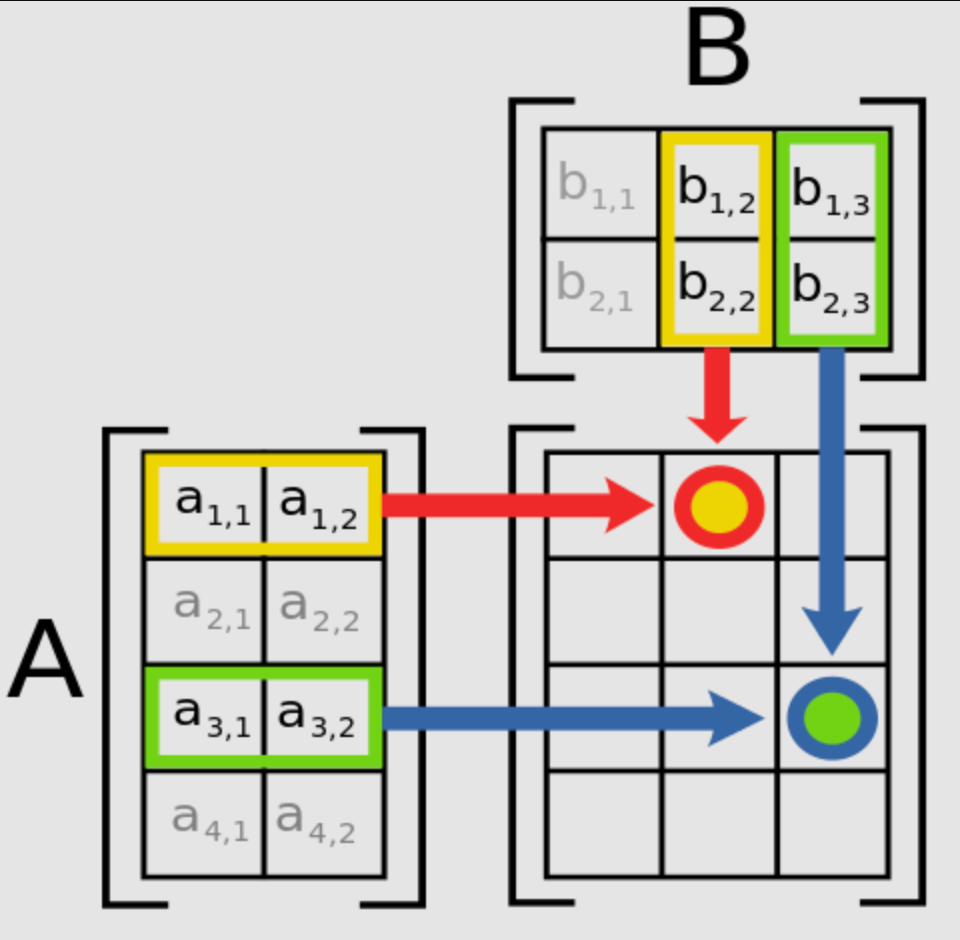
值得一提的是矩阵乘法运算,该运算仅当第一个矩阵 的列数和另一个矩阵
的行数相等时才能定义。如果
是一个
的矩阵,
是一个
矩阵,它们的乘积是一个
的矩阵,如下图所示。
例如:
矩阵的乘法满足结合律和对矩阵加法的分配律:
结合律: 。
左分配律: 。
右分配律: 。
矩阵乘法不满足交换律。一般情况下,矩阵 和
的乘积
存在,但
不一定存在,即便
存在,大多数时候
。
矩阵乘法的一个基本应用是在线性方程组上。线性方程组是方程组的一种,它符合以下的形式:
运用矩阵的方式,可以将线性方程组写成一个向量方程:
其中, 是由方程组里未知数的系数排成的
矩阵,
是含有
个元素的行向量,
是含有
个元素的行向量。
矩阵是线性变换(保持向量加法和标量乘法的函数)的便利表达法。矩阵乘法的本质在联系到线性变换的时候最能体现,因为矩阵乘法和线性变换的合成有以下的联系,即每个的矩阵
都代表了一个从
射到
的线性变换。如果无法理解上面这些内容,推荐大家看看B站上名为《线性代数的本质》的视频,相信这套视频会让你对线性代数有一个更好的认知。
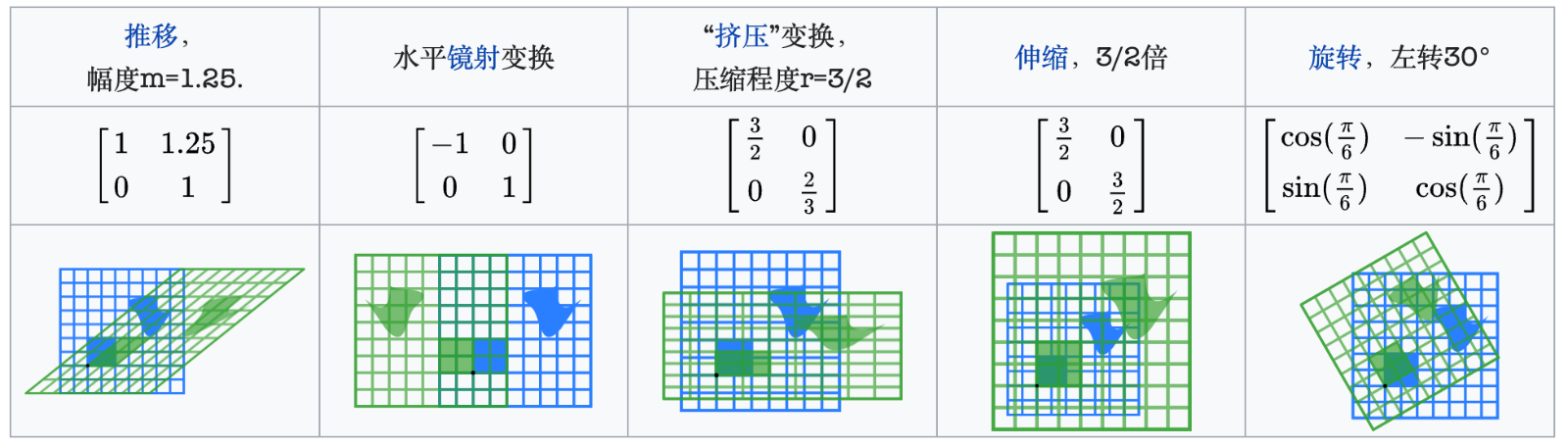
下图是一个来自于维基百科的例子,图中展示了一些典型的二维实平面上的线性变换对平面向量(图形)造成的效果以及它们对应的二维矩阵,其中每个线性变换将蓝色图形映射成绿色图形;平面的原点 用黑点表示。矩阵对象
NumPy 中提供了专门用于线性代数(linear algebra)的模块和表示矩阵的类型matrix,当然我们通过二维数组也可以表示一个矩阵,官方并不推荐使用matrix类而是建议使用二维数组,而且有可能在将来的版本中会移除matrix类。无论如何,利用这些已经封装好的类和函数,我们可以轻松愉快的实现很多对矩阵的操作。
我们可以通过下面的代码来创建矩阵(matrix)对象。
代码:
m1 = np.matrix('1 2 3; 4 5 6')
m1
说明:
matrix构造器可以传入类数组对象也可以传入字符串来构造矩阵对象。
输出:
matrix([[1, 2, 3],
[4, 5, 6]])
代码:
m2 = np.asmatrix(np.array([[1, 1], [2, 2], [3, 3]]))
m2
说明:
asmatrix函数也可以用mat函数代替,这两个函数其实是同一个函数。
输出:
matrix([[1, 1],
[2, 2],
[3, 3]])
代码:
m1 * m2
输出:
matrix([[14, 14],
[32, 32]])
说明:注意
matrix对象和ndarray对象乘法运算的差别,matrix对象的*运算是矩阵乘法运算。如果两个二维数组要做矩阵乘法运算,应该使用@运算符或matmul函数,而不是*运算符。
矩阵对象的属性如下表所示。
| 属性 | 说明 |
|---|---|
A | 获取矩阵对象对应的ndarray对象 |
A1 | 获取矩阵对象对应的扁平化后的ndarray对象 |
I | 可逆矩阵的逆矩阵 |
T | 矩阵的转置 |
H | 矩阵的共轭转置 |
shape | 矩阵的形状 |
size | 矩阵元素的个数 |
矩阵对象的方法跟之前讲过的ndarray数组对象的方法基本差不多,此处不再进行赘述。
线性代数模块
NumPy 的linalg模块中有一组标准的矩阵分解运算以及诸如求逆和行列式之类的函数,它们跟 MATLAB 和 R 等语言所使用的是相同的行业标准线性代数库,下面的表格列出了numpy以及linalg模块中一些常用的线性代数相关函数。
| 函数 | 说明 |
|---|---|
diag | 以一维数组的形式返回方阵的对角线元素或将一维数组转换为方阵(非对角元素元素为0) |
matmul | 矩阵乘法运算 |
trace | 计算对角线元素的和 |
norm | 求矩阵或向量的范数 |
det | 计算行列式的值 |
matrix_rank | 计算矩阵的秩 |
eig | 计算矩阵的特征值(eigenvalue)和特征向量(eigenvector) |
inv | 计算非奇异矩阵( $\small{n}$ 阶方阵)的逆矩阵 |
pinv | 计算矩阵的摩尔-彭若斯(Moore-Penrose)广义逆 |
qr | QR分解(把矩阵分解成一个正交矩阵与一个上三角矩阵的积) |
svd | 计算奇异值分解(singular value decomposition) |
solve | 解线性方程组 $\small{\boldsymbol{Ax}=\boldsymbol{b}}$,其中 $\small{\boldsymbol{A}}$ 是一个方阵 |
lstsq | 计算 $\small{\boldsymbol{Ax}=\boldsymbol{b}}$ 的最小二乘解 |
下面我们简单尝试一下上面的函数,先试一试求逆矩阵。
代码:
m3 = np.array([[1., 2.], [3., 4.]]) m4 = np.linalg.inv(m3) m4
输出:
array([[-2. , 1. ], [ 1.5, -0.5]])
代码:
np.around(m3 @ m4)
说明:
around函数对数组元素进行四舍五入操作,默认小数点后面的位数为0。
输出:
array([[1., 0.], [0., 1.]])
说明:矩阵和它的逆矩阵做矩阵乘法会得到单位矩阵。
计算行列式的值。
代码:
m5 = np.array([[1, 3, 5], [2, 4, 6], [4, 7, 9]]) np.linalg.det(m5)
输出:
2
计算矩阵的秩。
代码:
np.linalg.matrix_rank(m5)
输出:
3
求解线性方程组。
对于上面的线性方程组,我们可以用矩阵的形式来表示它,如下所示。
线性方程组有唯一解的条件:系数矩阵 的秩等于增广矩阵
的秩,而且跟未知数的个数相同。
代码:
A = np.array([[1, 2, 1], [3, 7, 2], [2, 2, 1]]) b = np.array([8, 23, 9]).reshape(-1, 1) print(np.linalg.matrix_rank(A)) print(np.linalg.matrix_rank(np.hstack((A, b))))
说明:使用数组对象的
reshape方法调形时,如果其中一个参数为-1,那么该维度有多少个元素是通过数组元素个数(size属性)和其他维度的元素个数自动计算出来的。
输出:
3 3
代码:
np.linalg.solve(A, b)
输出:
array([[1.], [2.], [3.]])
说明:上面的结果表示,线性方程组的解为:
。
下面是另一种求解线性方程组的方法,大家可以停下来思考下为什么。
代码:
np.linalg.inv(A) @ b
输出:
array([[1.], [2.], [3.]])
多项式
除了数组,NumPy 中还封装了用于多项式(polynomial)运算的数据类型。多项式是变量的整数次幂与系数的乘积之和,形如:
在 NumPy 1.4版本之前,我们可以用poly1d类型来表示多项式,目前它仍然可用,但是官方提供了新的模块numpy.polynomial,它除了支持基本的幂级数多项式外,还可以支持切比雪夫多项式、拉盖尔多项式等。
创建多项式对象
创建poly1d对象,例如: 。
代码:
p1 = np.poly1d([3, 2, 1]) p2 = np.poly1d([1, 2, 3]) print(p1) print(p2)
输出:
2 3 x + 2 x + 1 2 1 x + 2 x + 3
多项式的操作
获取多项式的系数
代码:
print(p1.coefficients) print(p2.coeffs)
输出:
[3 2 1] [1 2 3]
两个多项式的四则运算
代码:
print(p1 + p2) print(p1 * p2)
输出:
2 4 x + 4 x + 4 4 3 2 3 x + 8 x + 14 x + 8 x + 3
带入 $\small{x}$ 求多项式的值
代码:
print(p1(3)) print(p2(3))
输出:
34 18
多项式求导和不定积分
代码:
print(p1.deriv()) print(p1.integ())
输出:
6 x + 2 3 2 1 x + 1 x + 1 x
求多项式的根
例如有多项式,多项式的根即一元二次方程
的解。
代码:
p3 = np.poly1d([1, 3, 2]) print(p3.roots)
输出:
[-2. -1.]
如果使用numpy.polynomial模块的Polynomial类来表示多项式对象,那么对应的操作如下所示。
代码:
from numpy.polynomial import Polynomial p3 = Polynomial((2, 3, 1)) print(p3) # 输出多项式 print(p3(3)) # 令x=3,计算多项式的值 print(p3.roots()) # 计算多项式的根 print(p3.degree()) # 获得多项式的次数 print(p3.deriv()) # 求导 print(p3.integ()) # 求不定积分
输出:
2.0 + 3.0·x + 1.0·x² 20.0 [-2. -1.] 2 3.0 + 2.0·x 0.0 + 2.0·x + 1.5·x² + 0.33333333·x³
最小二乘解
Polynomial类还有一个名为fit的类方法,它可以给多项式求最小二乘解。所谓最小二乘解(least-squares solution),是用最小二乘法通过最小化误差的平方和来寻找数据的最佳匹配函数的系数。假设多项式为 ,最小二乘解就是让下面的残差平方和
达到最小的
和
。
例如,我们想利用收集到的月收入和网购支出的历史数据来建立一个预测模型,以达到通过某人的月收入预测他网购支出金额的目标,下面是我们收集到的收入和网购支出的数据,保存在两个数组中。
x = np.array([ 25000, 15850, 15500, 20500, 22000, 20010, 26050, 12500, 18500, 27300, 15000, 8300, 23320, 5250, 5800, 9100, 4800, 16000, 28500, 32000, 31300, 10800, 6750, 6020, 13300, 30020, 3200, 17300, 8835, 3500 ]) y = np.array([ 2599, 1400, 1120, 2560, 1900, 1200, 2320, 800, 1650, 2200, 980, 580, 1885, 600, 400, 800, 420, 1380, 1980, 3999, 3800, 725, 520, 420, 1200, 4020, 350, 1500, 560, 500 ])
我们可以先绘制散点图来了解两组数据是否具有正相关或负相关关系。正相关意味着数组x中较大的值对应到数组y中也是较大的值,而负相关则意味着数组x中较大的值对应到数组y中较小的值。
import matplotlib.pyplot as plt plt.figure(dpi=120) plt.scatter(x, y, color='blue') plt.show()
输出:
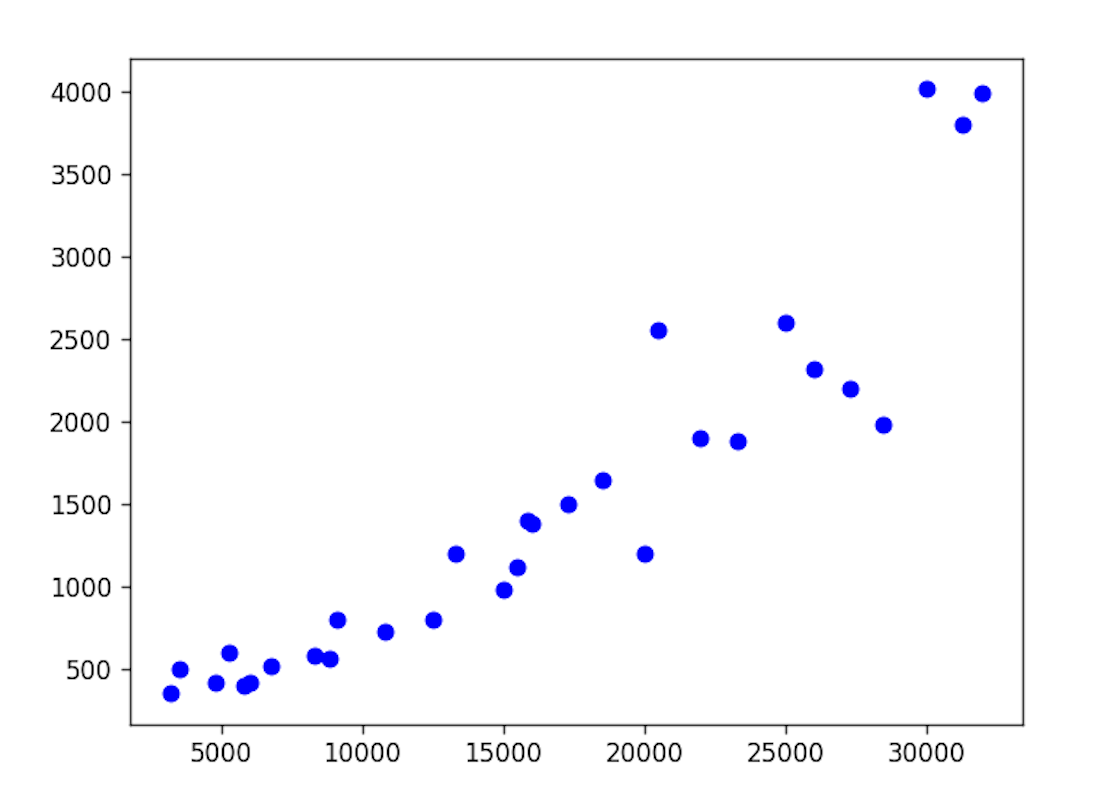
如果需要定量的研究两组数据的相关性,我们可以计算协方差或相关系数,对应的 NumPy 函数分别是cov和corrcoef。
代码:
np.corrcoef(x, y)
输出:
array([[1. , 0.92275889], [0.92275889, 1. ]])
说明:相关系数是一个
-1到1之间的值,越靠近1说明正相关性越强,越靠近-1说明负相关性越强,靠近0则说明两组数据没有明显的相关性。上面月收入和网购支出之间的相关系数是0.92275889,说明二者是强正相关关系。
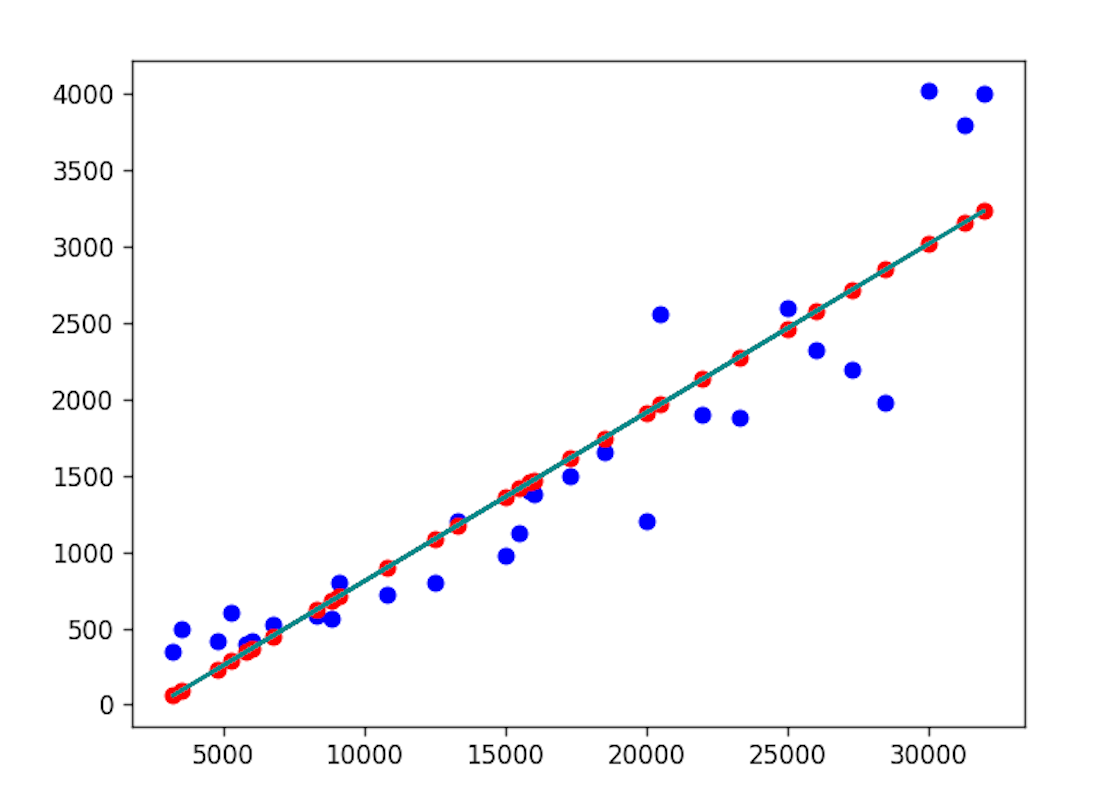
通过上面的操作,我们确定了收入和网购支出之前存在强正相关关系,于是我们用这些数据来创建一个回归模型,找出一条能够很好的拟合这些数据点的直线。这里,我们就可以用到上面提到的fit方法,具体的代码如下所示。
代码:
from numpy.polynomial import Polynomial Polynomial.fit(x, y, deg=1).convert().coef
说明:
deg=1说明回归模型最高次项就是1次项,回归模型形如;如果要生一个类似于
的模型,就需要设置
deg=2,以此类推。
输出:
array([-2.94883437e+02, 1.10333716e-01])
根据上面输出的结果,我们的回归方程应该是 。我们将这个回归方程绘制到刚才的散点图上,红色的点是我们的预测值,蓝色的点是历史数据,也就是真实值。
代码:
import matplotlib.pyplot as plt plt.scatter(x, y, color='blue') plt.scatter(x, 0.110333716 * x - 294.883437, color='red') plt.plot(x, 0.110333716 * x - 294.883437, color='darkcyan') plt.show()
输出:
如果不使用Polynomial类型的fit方法,我们也可以通过 NumPy 提供的polyfit函数来完成同样的操作,有兴趣的读者可以自行研究。
说明:本章部分图片来自于维基百科。

评论